Contents

• Directed Graph Traversal

Directed-Graph-Traversal

Topological Order, Postorder, Reverse Postorder

Algo 4.2 Directed Graphs

Depth-first orders: Depth-first search search visits each vertex exactly once. Three vertex orderings are of interest in typical applications:

Preorder: Put the vertex on a queue before the recursive calls.

Postorder: Put the vertex on a queue after the recursive calls.

Reverse postorder: Put the vertex on a stack after the recursive calls. 

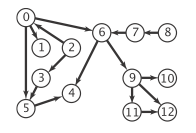
Example of topological order, postorder: Algorithms 4.2

Topological Order:

topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.